Matematikte ondalık gösterim nedir?

Ondalık gösterim taban olarak 10 sayısının ele alınarak kesirli bir sayının gösteriliş şeklini ifade eder. Matematik tarihinde matematiksel işlemler sayesinde ondalık gösterim kolayca yapılabilir. Ondalık sayılar esasında kesirleri temsil etseler bile belirli noktalarda matematiksel işlemleri kolaylaştırırlar.

Öğrenciler ondalık sayılara 4. sınıfta yüzeysel şekilde giriş yaparlar. 5. sınıf ondalık gösterimde temel atılır. 6. sınıf ondalık gösterimde ise kapsamlı sorulara ve problemlere geçiş yapılır. Bu sebeple ondalık gösterim testi çözmek istediğinizde test seviyelerine dikkat etmelisiniz.

İçerikler

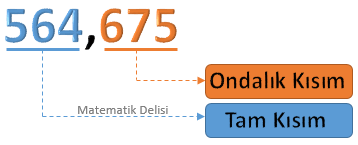
Ondalık gösterim nedir?

Ondalık gösterim, 10 tabanını kullanan bir kesrin temsili anlamına gelir. Bir başka ifadeyle bir kesir sayısı ondalık basamak değerine göre ondalık gösterimde yazılır. Ondalık sayı, bir tam sayı ve ondalık virgül olarak adlandırılan kesir kısmı olmak üzere iki bölümden oluşur.

Ondalık sayılarda rakamlar 0-9 aralığında olur. Ondalık sayıların tabanı 10 olduğundan basamak değer sistemi ona uygun olarak yazılır. Virgülden önceki basamak birler, onlar ve yüzler şeklinde ilerler. Virgülden sonrası ise farklı biçimlerde telaffuz edilirler.

Kesirlerin ondalık gösterimi söz konusu olduğunda ondalıktan sonraki basamak sayının kesirli kısmına denk gelir. Örnek vermek gerekirse 0,53 sayısında 5 onluk ve 3 yüzlük bulunur. 0,53 sayısı aslında 5/10 + 3/100 demektir. Gerek duyulduğunda ondalık sayı kesre dönüştürülebilir.

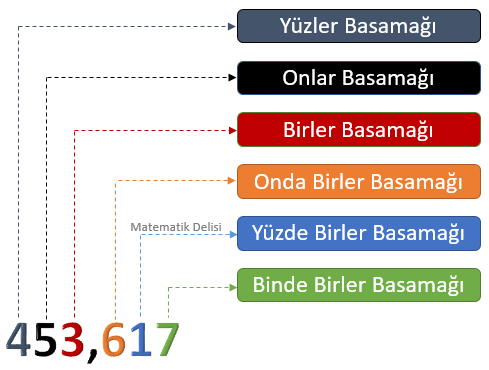
Ondalık gösterim basamak adları nelerdir?

Ondalık gösterim basamak adları virgülden önce ve sonra olacak şekilde ikiye ayrılır. Sayılar ifade edilirken virgülün solu ve sağı ayrı ayrı ele alınırlar. Ondalık gösterim basamak değerlerinde virgülün solundaki sayılar birler, onlar, yüzler ve binler şeklinde ilerler.

Virgülün sağı kesirli kısmı ifade eder. Ondalık gösterim basamak adları ise onda birler, yüzde birler ve binde birler şeklinde ilerler. Ondalık gösterim basamak değerleri özellikle kesri ondalık gösterime çevirme konusunda önemlidir ve doğru şekilde ifade edilmeleri gerekir.

Matematik ondalık gösterimler söz konusuysa basit bir şekilde düşünmeyi teşvik eder. Kesirli kısmın hangi değere denk geldiğini bilmek sayıyı çözümlemede yeterlidir. Ondalık gösterim basamak adları çözümleme konusunda işinizi epey bir kolaylaştırır.

Ondalık gösterimle çarpma işlemi nasıl yapılır?

Ondalık gösterimle çarpma işlemi tam sayılarda çarpma işlemine oldukça benzerdir. Normal yaşantınızda ondalık sayılarla pek uğraşmadığınızı düşünseniz bile gerçek böyle değildir. Küsuratlı olan her sayıda aslında ondalık gösterimle çarpma işlemi yaparsınız.

15 ile 7,5 sayılarını çarpacağınızı düşünelim. İlk olarak ondalık sayıda yer alan virgülü yok sayarak iki sayının çarpımını gerçekleştirmelisiniz.
15 ile 75 sayılarını çarptığınızda 1125 sayısını elde edersiniz. Bu sayıyı elde ettikten sonra ondalık sayıda virgülün sağındaki rakam miktarına bakmalısınız.
7,5 sayısında virgülün sağ kısmında tek bir rakam vardır. Doğal olarak 15 ile 7,5 sayısını çarptığınızda elde edeceğiniz sayıda virgülün sağ tarafında tek bir rakam yer almalıdır.
15 ile 75 sayılarını çarptığınızda 1125 elde etmiştiniz. Doğal olarak 15 ile 7,5 sayılarını çarptığınızda elde edeceğiniz sonuç 112,5 şeklinde olacaktır.

Ondalık gösterim basamak değerlerini biliyorsanız ondalık gösterimle çarpma işlemi gerçekleştirmek çok basittir. Bazı durumlarda ise çarpma işleminin sonucuna uygun olarak yuvarlama yapmanız gerekebilir. Ondalık gösterim yuvarlama çok zor bir işlem değildir.

Ondalık gösterim yuvarlama işlemi nasıl yapılır?

Ondalık gösterim yuvarlama işlemi matematiksel işlemlerde sonucu netleştirmek için yapılır. Doğru basamakta yer alan sayıyı yuvarladığınızda istediğiniz sonucu elde edersiniz. Rakam 5’ten küçükse aşağı doğru, büyük veya eşitse yukarı doğru yuvarlama yapmalısınız.

Ondalık sayılarda yuvarlama işlemini en yakın sayıya doğru yapabilirsiniz. Örneğin, 345,62 sayısını yuvarladığınızda 346 olarak yazabilirsiniz.
Ondalık sayılarda yuvarlama işlemini en yakın 10’un katına doğru yapabilirsiniz. 345,62 sayısını 10’un katına doğru yuvarlamak istediğinizde 345,60 sonucunu elde edersiniz.

Ondalık gösterim yuvarlama işlemini hangi yöne doğru yapmanız gerektiğine dikkatli karar vermelisiniz. Bir denklem veya problem çözerken genelde işe yarar değere yönelik yuvarlama yapılır. Ondalık sayılarda yuvarlama matematiksel işlemleri daha kolay hale getirir.

Devirli ondalık gösterim ne anlama gelir?

Devirli ondalık gösterim, ondalık sayılarda virgülden sonraki kısmın tekrarlanması durumunda oluşan sayıdır. Sayıda yer alan duruma göre devirli ondalık sayı sonsuz basamaklı olabilir. Ondalık gösterim çözümleme yaparken tekrarlanan kısma dikkat etmek gerekir.

Bir sayının devirli ondalık gösterim kapsamına dahil edilebilmesi için ondalık basamağın sağından sonra sabit bir ifade (terim) dizisinin yer alması gerekir. Örnek vermek gerekirse 0,111111… şeklinde devam eden bir sayı devirli ondalık sayı kapsamında ele alınır.

Devirli ondalık gösterim yapılırken devreden sayıların üst kısmına çizgi (-) işareti konulur. Üzerinde çizgi yer alan sayılar sürekli tekrarlanırlar. Ondalık gösterim çözümleme sırasında devreden sayılarda yapılan işlemler standart sayılarından çok daha farklıdırlar.

Kesrin ondalık gösterimi nasıl yapılır?

Kesrin ondalık gösterimi herhangi bir kesirli sayıyı tam sayıyla birlikte ondalık şekilde yazmak anlamına gelir. Dönüştürme yapılırken genelde bölme işlemi uygulanır. Ancak kesrin ondalık gösterimi için birbirinden farklı işlevsel yöntemler kullanabilmek mümkündür.

Kesir biçiminde olan bir sayıda pay ve payda olmak üzere iki farklı kısım bulunur. Kesri ondalık gösterime çevirmek için genelde pay paydaya bölünür. Kesirlerin ondalık gösterimini sağlıklı bir şekilde yapmak istiyorsanız bölmeyle uygulanan uzun yönteme bağlı kalmalısınız.

1. Kesrin ondalık gösteriminde uzun yöntem

Kesri ondalık gösterime çevirmek için uygulanan uzun yöntem aslında standart bölme işlemidir. Bölme işlemini yaparken hangi kısımları tam sayı olarak yazacağınızı bilmeniz yeterlidir. Uzun yöntemin nasıl uygulanacağını örnek üzerinden kontrol edebilirsiniz.

5/8 olarak ifade ettiğimiz sayıda 5 rakamı pay ve 8 rakamı paydadır. Ondalık sayıya dönüştürmek için 5’i bölünen ve 8’i bölen olarak kabul etmelisiniz.
5/8 sayısı için payda paydan büyük olduğundan doğrudan bölme işlemi yapılamaz. Bölme yapabilmek için 5 rakamının sağına bir adet 0 eklemelisiniz.
50 rakamının sağına 0 eklediğinizden bölüm kısmına 0 yazmalı ve sonra onu ondalık olarak ifade etmek için virgül (,) koyup bölme işlemine başlamalısınız.
Şimdi yapmanız gereken 50 sayısının içerisinde kaç tane 8 olduğunu düşünmektir. 8’i herhangi bir sayıyla çarpıp ilerleyebilirsiniz. 6 ile çarptığınızda 48 sayısını elde edersiniz.
Bölüm kısmında yer alan sayı şimdi 0,6 şeklindedir. Elimizde ise kalan olarak 2 rakamı vardır. 2 rakamının sağına 0 ekleyerek bölme işlemine devam etmelisiniz.
Şu an elinizdeki yeni pay 20’dir. 20’nin içinde 8 sayısını kaç kez olduğunu düşünmelisiniz. 2 ile çarptığınızda 16 elde edersiniz. Bölme kısmı artık 0,62’dir ve elde kalan 4’tür.
Kalan 4 rakamının sağına 0 ekledikten sonra 40 sayısını elde edersiniz. 5 ile çarptığınızda 40 elde edersiniz ve kalan olmadığından dönüştürme işlemini tamamlarsınız.

5/8 kesirli sayısının ondalık olarak yazılışı 0,625 şeklindedir. Kesirlerin ondalık gösteriminde bölme işlemi bazen devirli sonuçlar verebilir. Bu durumda tekrar eden sayıları devirli olarak göstermeniz yeterli olacaktır. Örneğin, 5/11 sayısı 0,454545 şeklinde devirli ilerler.

2. Kesrin ondalık gösteriminde kısa yöntem

Kesrin ondalık gösterimi için kullanılan alternatif yöntem biraz daha pratiktir. Bunun için kesrin paydasını 10, 100, 1000 gibi 10’un katı olacak şekilde yazmaya çalışmalısınız. Pratik bir yöntem olmasına rağmen biraz daha fazla matematik bilgisi gerektiren bir işlemdir.

5/8 kesirli sayısını ondalık sayı olarak yazmak için kısa yöntemi kullanacaksanız hem pay hem de paydayı aynı sayıyla çarpmalı ve paydada 10’un katını elde etmelisiniz.
5/8 kesirli sayısında payda 8’dir. 8 sayısı 1000 sayısının içerisinde 125 kez vardır. Doğal olarak kesrin payı olan 5 rakamını 125 sayısıyla çarpmalısınız.
5 ile 125 sayısını çarptığınızda 625 sayısını elde etmiş olursunuz. Elinizdeki yeni sayı 625/1000 şeklindedir ve bunu kolayca ondalık olarak yazabilirsiniz.
Kesirli sayımızın paydası 1000’dir. Paydada 3 tane sıfırın olması virgülden sonra 3 tane rakam olacağı anlamına gelir. Bu durumda ondalık sayımız 0,625 olacaktır.

Matematik ondalık gösterim konusunda işinizi kolaylaştırır. Ancak pratik işlem yapabilme konusunda alışkanlık edinmeniz önemlidir. Sonrasında rasyonel sayılar dahil olmak üzere dönüştürmeye uygun dilediğiniz sayı türünü ondalık sayı olarak yazabilirsiniz.

Ondalık gösterim kesre nasıl çevrilir?

Ondalık gösterim çözümleme işlemini ayrıntılarıyla beraber öğrendikten sonra tam tersi bir işlem yapabilirsiniz. Bir başka ifadeyle ondalık gösterimi kesre çevirmek için çarpma işlemi uygulamalısınız. Ondalık gösterimi kesre çevirmek için basit adımları takip etmek yeterlidir.

0,35 sayısını kesre dönüştürmek için ilk olarak ondalık sayıyı paydası 1 olacak şekilde yeniden yazmalısınız. Böylece gerekli işlemleri kolaylaştırmış olursunuz.
0,35/1 sayısındaki payda kısmını 10’un katı haline dönüştürmelisiniz. Bunun için paydadaki 1 sayısının yanına ondalıkta virgülün sağındaki rakam kadar 0 eklemelisiniz.
Şu an ulaştığınız sayı 35/100 olmalıdır. 35/100 sayısını sadeleştirdiğinizde ondalık gösterimi kesre çevirme işlemini başarıyla tamamlamış olursunuz.
35 ve 100 sayıları 5’in katıdırlar. Her ikisini 5’e böldüğünüzde 7 ve 20 sayılarını elde edersiniz. 0,35 sayısının kesirle gösterilmiş hali 7/20 şeklindedir.

Matematik ondalık gösterim işlemlerini olabildiğince basitleştirir. Özellikle tam sayı kısmı 0 olan sayıları zorlanmadan dönüştürebilirsiniz. Tam sayı kısmı 0’dan farklı olan sayılarda ise dönüştürme işleminin ardından kesir kısmına tam değerini yazmanız gerekir.

Karekök sayılarda ondalık gösterim nasıl yapılır?

Karekök sayılarda ondalık gösterim aslında ondalık formdaki sayıların karekökünü bulma işlemidir. Söz konusu işlemi yapabilmek için matematiksel işlemleri içeren birkaç prosedürü takip etmek gerekir. Ancak standart sayılara göre biraz daha ileri seviye işlemler yapılır.

√1,96 sayısının hangi sayıya eşit olduğunu bulmak istiyorsanız ondalık sayıdan kesre dönüştürme yapmalısınız. Sonrasında kesrin karekökünü alarak sonuca ulaşabilirsiniz.
1,96 sayısını kesirli sayıya dönüştürdüğünüzde 196/100 sayısını elde edersiniz. Şimdi yapmanız gereken söz konusu kesirli sayının karekökünü almaktır.
√196/100 sayısı aslında √196/√100 sayısıdır. 100 sayısı 10’un, 196 sayısı ise 14’ün tam karesidir. Doğal olarak elde edilecek sonuç 14/10 şeklindedir.
Kesri ondalık sayıya dönüştürme işlemi yaptığınızda 14/10 sayısı 1,4’e denk gelir. Bir başka ifadeyle √1,96 sayısının ondalık sayı hali 1,4 olacaktır.

Karekök sayılarda ondalık gösterim karmaşık bir işlem gibi gözükebilir. Ancak sayıların tam karelerini bildiğinizde epey basittir. Aynı zamanda karekök sayılarda ondalık gösterim için çarpma ve bölme işlemlerini yapmada yeteri kadar pratik yapmış olmanız önemlidir.

Rasyonel sayılarda ondalık gösterim nasıl yapılır?

Rasyonel sayılarda ondalık gösterim, rasyonel sayıyı aynı matematiksel değere sahip ondalık sayıya dönüştürmek anlamına gelir. Bölme işlemi yapılarak rasyonel sayılar ondalık olarak gösterilebilirler. Çevirme yapabilmek için matematikte dört işlem bilgisi yeterlidir.

7/5 bir rasyonel sayıdır ve ondalık olarak yazmak için pratik bir yöntem kullanabilirsiniz. İlk olarak paydayı 10’un katına eşitlemeniz ve payı aynı sayıyla çarpmalısınız.
7/5 rasyonel sayısında payda 5’tir ve onu 10’a eşitlemek için 2 ile çarpmalısınız. Benzer şekilde pay 7’dir ve onu 2 ile çarparak 14 sayısını elde edebilirsiniz.
Elinizdeki sayı artık 14/10 şeklindedir. Payda 10’dur ve sadece bir tane 0 içerir. Dolayısıyla virgülden sonraki kısım tek rakamdan oluşur ve elde edeceğiniz ondalık sayı 1,4’tür.

Rasyonel sayılar ondalık gösterim için idealdirler. Aşırı fazla matematiksel işlemlere gerek yoktur. Bazı durumlarda ise sayıları sadeleştirmek ve sonra 10’un katına eşitlemek gerekebilir. Rasyonel sayılar ondalık gösterimde işlem yapacak kişiye çok fazla zorluk çıkartmazlar.

Devirli ondalık gösterim nasıl rasyonel sayıya dönüştürülür?

Devirli ondalık gösterimi rasyonel sayıya çevirme işlemini yapabilmek için temel düzeyde ondalık sayı dönüştürme yöntemlerini bilmeniz yeterlidir. Tek yapmanız gereken tekrar eden kısmı belirlemek ve onun üzerinden çeşitli işlemler yaparak ilerlemektir.

0,8888… sayısında kolayca fark edebileceğiniz gibi 8 sayısı devreden durumundadır. Devirli ondalık gösterimi rasyonel sayıya çevirme yaparken 8 üzerinden ilerlemelisiniz.
0,8888… sayısının birler basamağına (virgülün solundaki ilk rakam) hemen 8 sayısını koyun. Aslında yaptığınız işlem 0,8888… sayısını 10 ile çarpmaktır.
0,8888… sayısına “x” değerini atamalısınız. Bu durumda 8,888 sayısı 10x olacaktır. Şimdi yapmanız gereken işlem ise “10x” değerinden “x” değerini çıkartmaktır.
8,888 sayısından 0,8888 sayısını çıkarttığınızda sonuç 8 olur. Bu aynı zamanda 8 sayısının 9x değerine eşit olduğu anlamına gelir. 9x = 8,0 formülünden x = 8/9 değeri bulunur.

Devirli ondalık gösterimi rasyonel sayıya çevirme işleminin uzun yöntemi bu şekildedir. Çok daha kısa olan yöntemde ise devreden ondalık sayının basamakları sayılarak ilerlenir. Kısa yöntem karmaşık olsa bile ileri düzey problemler ve denklemlerde daha faydalıdır.

Ondalık sayılar hangi sınıftan itibaren öğrenilir?

Ondalık sayılar genel olarak 4. sınıftan itibaren karşılaşılan bir alandır. Ancak konuya tam anlamıyla giriş 5. ve 6. sınıfta olur. 5. sınıf ondalık gösterimde temel için gerekli olan adımlara yer verilir. 6. sınıf ondalık gösterimde ise denklemler ve problemler devreye girerler.

5. sınıf ondalık gösterim, ondalık sayıların okunması ve yazılması gibi temel düzeyde bilgileri verir. Sonrasında ise basamak değerleri, kesir kısmı ve tam kısmı detaylarına değinilir. Ondalık sayıları tanımak ve onlarla çeşitli işlemler yapmayı öğrenmek için başlangıç noktasıdır.

6. sınıf ondalık gösterim ise işlemleri yoğunlaştırır. Çözümleme, yuvarlama, çarpma ve bölme gibi işlemler pratiğe dökülür. Sonrasında ise basit düzeyde problemlere ve denklemlere geçiş yapılabilir. En çok kullanılacak bilgiler ise çarpma ve bölme işlemleriyle alakalıdır.

5. sınıf ondalık gösterim örnekleri

5. sınıf ondalık sayı örnekleri temel düzeydedirler. Daha çok okunuş ve yazılışla ilgili sorulara denk gelebilirsiniz. 5. sınıf için ondalık gösterim örneklerini incelediğinizde ondalık sayıları anlamak adına temel düzeyde bilgi gereksiniminin yeterli olduğunu görebilirsiniz.

Soru: 2,07 sayısının okunuşu aşağıdakilerden hangisidir?

Cevap: Ondalık sayılar okunurken önce tam sayı kısmı ifade edilir. 2,07 sayısında iki tane ondalık basamak vardır. Bu sebeple okunuşu “iki tam yüzde yedi” şeklindedir.

Soru: Okunuşu “üç tam yüzde otuz dört” olan sayı aşağıdakilerden hangisidir?

Cevap: Ondalık sayılar yazılırken önce tam sayı kısmı yazılmalıdır. “Üç tam yüzde otuz dört” olarak ifade edilen sayıda iki tane ondalık basamak vardır. Dolayısıyla sayı “3,34” şeklindedir.

Soru: 5/10 kesrinin ondalık sayı olarak yazılışı hangisidir?

Cevap: Kesirli sayıyı ondalık sayıya dönüştürürken yapılacak işlemleri takip etmelisiniz. 5/10 kesrinde payda paydan büyüktür. Bu sebeple tam sayı basamağının 0 olması gerekir. Ondalık basamak kısmında ise tek bir sayı yer almalıdır. Dolayısıyla sayı “0,5” şeklindedir.

6. sınıf ondalık gösterim örnekleri

6. sınıf ondalık sayı örnekleri bir önceki sınıftan biraz daha ileri düzeydedir. Çünkü ondalık gösterim örnekleriyle oluşturulan problemlere giriş yapılır. Problemleri çözmek bölme ve çarpma işleminden çok daha fazlasını gerektirdiğinden sorular biraz daha zor olur.

Soru: Kredi kartı faturası 848,63 TL gelen Ali bankaya 850 TL’lik ödeme yapmıştır. Ali’nin bankadan alacağı para üstü ne kadardır?

Cevap: Ali bankaya 850 TL ödemiştir. Toplam borcu ise 848,63 TL’dir. Dolayısıyla geri alacağı miktarı bulmak için 850’den 848,63 çıkartmak gerekir. Cevap 1,37 olmalıdır.

Soru: Bir mobil operatörde SMS göndermenin ücreti 54 kuruştur. Ayşe geçtiğimiz ay 29 SMS göndermiştir. Ödemesi gereken ücret ne kadardır?

Cevap: 1 adet SMS ücreti 54 kuruştur ve Ayşe toplamda 29 SMS göndermiştir. Cevabı bulabilmek için 54 ile 29 sayılarını çarpmak yeterlidir. Dolayısıyla cevap 156,60 TL olacaktır.

Soru: A + 4,5 = 9,3 şeklinde bir denklem mevcuttur. B – A = 2,2 ve B – C = 1,80 ise “(A + C) x B” işleminin sonucu nedir?

Cevap: Matematiksel işlemleri tamamladığınızda sırasıyla A, B ve C sayılarını bulursunuz. A sayısı 4,8 ve B sayısı 7’dir. C sayısı ise 5,20’dir. (A + C) x B işleminin sonucu 70 olacaktır.

Ondalık gösterim örneklerine baktığınızda çok daha farklı sorular bulabilirsiniz. Özel olarak oluşturulmuş ondalık gösterim testi bulursanız konuyu pekiştirmek daha kolay olabilir. Ondalık gösterim testi seçerken zorluk seviyelerine çok dikkat etmelisiniz.